Năm 2021, Quỹ VINIF đã gửi gắm mong ước về một vũ trũ hài hòa và sáng tạo trong Khối lịch 12 mặt của mình. Bạn có biết chăng khối đa diện đều 12 mặt ấy có một lịch sử hơn 4000 năm với biết bao câu chuyện, từ những suy tư sâu xa về triết học, những định lý toán học, những thiết kế kiến trúc đến cả những trò chơi may rủi; và cho đến tận năm 2020 nó vẫn là đề tài của một lời giải cho một giả thuyết toán học, một lời giải kết hợp giữa toán học lý thuyết và sức mạnh tính toán của các thuật toán tin học hiện đại nhất. Hãy cũng chúng tôi khám phá hành trình ấy nhé.

Vũ trụ hài hòa
Theo lịch sử, những đa diện đều sơ khai được tạo ra từ cách đây hơn 4000 năm và chúng được chạm khắc trên những khối đá, đó là những hình khối rất đều đặn và hài hòa: tất cả các mặt giống nhau, các cạnh giống nhau, các góc giống nhau (“Khối đa diện đều”, 2021). Một bộ sưu tập những hòn đá nhỏ được khắc thành những khối đã được tìm thấy ở Scotland và có niên đại trước cả nghìn năm so với thời đại của các nhà toán học Hy Lạp, đang được trưng bày trong bảo tàng Ashmolean ở Oxford, Anh Quốc. Chúng được đặt tên là khối tetrahedron (khối 4 mặt – tứ diện), hexahedron (khối 6 mặt – lục diện), octahedron (khối 8 mặt – bát diện) và docecahedron (khối 12 mặt – thập nhị diện), icosahedron (khối 20 mặt – nhị thập diện).
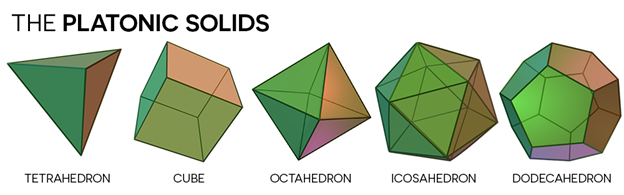
Nhưng phải đến khi nhà thiên văn học, toán học và triết học Platon xứ Hy Lạp đưa những tư tưởng triết học, gắn với những nguyên tố của vũ trụ thì các hình khối ấy mới trở nên nổi tiếng. Theo Platon thì năm đa diện đều này đại diện cho các yếu tố cơ bản trong vũ trụ: lửa – tứ diện, nước – nhị thập diện, không khí – bát diện, đất – lục diện và vũ trụ – thập nhị diện (Mickael Launay, 2016). Khối thập nhị diện với các mặt hình ngũ giác, Platon cho rằng nó biểu diễn hình dạng thật của Vũ Trụ. Tuy học thuyết này đã bị khoa học bác bỏ từ lâu, nhưng người ta vẫn quen gắn kết năm khối đa diện đều này với Platon và từ đó chúng đã được mang tên những khối đa diện Platon.
Liệu có thể có những khối đa diện khác không? 10 mặt chẳng hạn? Câu trả lời thật bất ngờ: không, chỉ có 5 khối đa diện ấy thôi. Và một chứng minh toán học đã được hoàn thiện từ thủa sơ khai của hình học, vào thế kỷ thứ 4 trước công nguyên do nhà toán học Theaetetus công bố!
- Mỗi đỉnh của khối đa diện phải là giao của ít nhất ba mặt.
- Tại mỗi đỉnh của khối đa diện, tổng các góc của các mặt phải nhỏ hơn 360°.
- Các góc tại tất cả các đỉnh của khối đa diện đều là bằng nhau do đó mỗi góc phải nhỏ hơn 360°/3=120°.
- Các đa giác đều có từ sáu cạnh trở lên có góc là 120° trở lên nên không thể là mặt của khối đa diện đều, do đó mối mặt của khối đa diện đều chỉ có thể là các tam giác đều, hình vuông hoặc ngũ giác đều. Cụ thể:
- Các mặt là tam giác đều: góc ở mỗi đỉnh của tam giác đều là 60°, do đó tại mỗi đỉnh chỉ có 3, 4, hoặc 5 góc của tam giác; tương ứng ta có các tứ diện đều, khối tám mặt đều và khối hai mươi mặt đều.
- Các mặt là hình vuông: góc ở đỉnh hình vuông là 90°, do đó chỉ có thể có ba mặt tại mỗi đỉnh ta có khối lập phương.
- Các mặt là ngũ giác đều: mỗi góc ở đỉnh là 108°; do đó chỉ có thể có đúng ba mặt tại một đỉnh, khi đó ta có khối mười hai mặt đều.
Một kết quả toán học đẹp như vậy đâu chỉ dừng lại ở một chứng minh, đã có nhiều nhà toán học tìm cách chứng minh Định lý 5 khối đa diện đều, trong đó cách chứng mình của nhà toán học nổi tiếng Euler – một chứng minh rất tinh tế, nó gắn liền với lý thuyết topo hình học, và đồ thị. Chìa khóa của chứng minh này là công thức Euler: V-E+F=2 trong đó V, E, F lần lượt là số đỉnh, số cạnh và số mặt của khối đa diện. (Các bạn hãy thử tự xây dựng chứng minh này nhé!).
Nhắc đến Euler, hẳn chúng ta sẽ nhớ ông là thủy tổ của lý thuyết đồ thị với bài toán 7 cây cầu ở thành phố Konisberg và chu trình Euler nổi tiếng. Nhưng có thể nói về chu trình Euler (đường đi qua tất cả các cạnh của đồ thị mỗi cạnh đúng một lần và quay về đỉnh xuất phát) mà không liên tưởng tới chu trình Hamilton (đường đi qua tất cả các đỉnh của đồ thị mỗi đỉnh đúng một lần và quay về đỉnh xuất phát) chăng? Hai loại chu trình tưởng rất tương tự nhau mà trở thành hai bài toán khác xa nhau vời vợi: bài toán tìm chu trình Euler rất dễ còn bài toán tìm chu trình Hamilton là bài toán siêu khó (trong lý thuyết tin học thì là bài toán NP- đầy đủ). Và điều bất ngờ là chu trình Hamilton có nguồn gốc gắn với khối đa diện đều! Năm 1859, William Rowan Hamilton đã đặt câu hỏi “Xuất phát từ một đỉnh của khối đa diện đều 20 mặt, hãy đi dọc theo các cạnh của khối đó sao cho đi qua tất cả các đỉnh khác, mỗi đỉnh đúng một lần sau đó quay về đỉnh xuất phát (“Hamiltonian path”, 2021). Thậm chí nó xuất phát từ khối đa diện đều 12 mặt: vì nguyên bản Hamilton phát biểu bằng: Hãy tìm một chu trình Hamilton của đồ thị cạnh của đa diện đều 12 mặt. Và các bạn biết không: đồ thị cạnh của nó chính là đồ thị của khối đa diện đều 20 mặt. Theo các bạn câu trả lời là có hay không?
Câu trả lời là có, cả 5 khối đa diện đều đều có chu trình Hamilton.
Nhưng! Nhưng hãy chú ý! Có một Giả thuyết toán học và người ta đã giải được nó cho cả 4 khối đa diện đều kia. Chỉ còn duy nhất khối vũ trụ 12 mặt là câu hỏi mở trong bao thập kỷ. Giả thuyết ấy vừa được giải vào năm 2020, không chỉ nhờ Toán học mà phải nhờ cả sức mạnh của Tin học, với khả năng tính toán phi thường của các thuật toán. Ta cùng khám phá nhé.
Giả thuyết Đường đi trên Khối đa diện đều:
Một chú kiến xuất phát từ 1 đỉnh của đa diện đều lồi, cứ đi thẳng, liệu có thể quay về đỉnh xuất phát mà không đi qua đỉnh nào khác không? Trong điều kiện đi thẳng là khi đi qua giao của 2 mặt nó bảo toàn các góc đối diện (hay khi lật hai mặt cho phẳng nhau thì đường đi là thẳng).

Đối với 4 hình đa diện đều là tứ diện đều, lục diện đều, bát diện đều, nhị thập diện đều, câu trả lời là chú kiến không thể quay về đỉnh xuất phát. Bất kì đường thẳng nào xuất phát từ một góc của 4 hình đa điện đó sẽ cắt một góc khác hoặc đi mãi không bao giờ quay trở về đúng điểm ban đầu. Vậy chỉ còn lại câu hỏi mở đối với khối thập nhị diện đều?
Lạ kỳ thay: Riêng với khối 12 mặt, câu trả lời là có. Không những thế, có vô số cách đi.
Vào tháng 5 năm 2020, trong bài báo Platonic Solids and High Genus Covers of Lattice Surfaces đăng trên tạp chí Experimental Mathematics (“Mathematicians Report New Discovery About the Dodecahedron”, 2020), các nhà khoa học Jayadev S. Athreya, David Aulicino, W. Patrick Hooper và Anja Randecker đã chứng minh rằng chỉ ra rằng có 31 tổ hợp/ nhánh tự nhiên (natural families) các đường đi trên mặt phẳng khối thập nhị diện.
Chứng minh này dựa trên việc nghiên cứu lưới và các phép đối xứng cùng với phép tịnh tiến mặt. Nhưng để hoàn tất các tính toán thì cần phải có các thuật toán tính toán với hàng tỷ đường đi phải xét.
Chứng minh này dựa trên việc nghiên cứu lưới và các phép đối xứng cùng với phép tịnh tiến mặt. Nhưng để hoàn tất các tính toán thì cần phải có các thuật toán tính toán với hàng tỷ đường đi phải xét. Nghiên cứu chỉ ra, để tìm hiểu các đường thẳng trên khối Platon, bạn có thể bắt đầu bằng cách cắt các góc của khối ra cho tới khi tạo được một mặt phẳng. Có thể sử dụng giấy để tạo ra mặt phẳng khối đa diện đều như trong hình bên dưới. Mặt phẳng này được các nhà toán học gọi là “lưới” (Net). Ví dụ, một lưới của khối lục diện đều là hình chữ T tạo thành bởi 6 hình vuông.

Hình dung chúng ta tạo phẳng các mặt khối thập nhị diện, và giờ chúng ta đi bộ dọc mặt phẳng này từ một đỉnh và tới một hướng đã lựa chọn. Cuối cùng, chúng ta sẽ tới cạnh tận cùng của lưới, tại điểm này con đường của chúng ta sẽ chuyển sang một khối đa diện khác (được gắn vào khối đa diện trước khi chúng ta cắt ra).
Dự án tính toán này được khởi nguồn từ năm 2016, khi Athreya – đại học Washington, và Aulicino trường Brooklyn College bắt đầu. Những nghiên cứu về mặt tịnh tiến với 10 bản sao của mỗi ngũ giác mang đến nhiều tính toán phức. Tuy nhiên đó lại là tiền đề cho phép ba nhà nghiên cứu Jayadev Athreya, David Aulicino và Patrick Hooper tiếp cận các học thuyết về mặt tịnh tiến. Bằng cách áp dụng một “Thuật toán phân tích các mặt tịnh tiến có tính đối xứng” của Myriam Finster, các nhà nghiên cứu có thể xác định tất cả các đường thẳng trên khối thập nhị diện từ một góc đến chính nó và phân loại các đường đi này thông qua các đối xứng ẩn của khối mặt phẳng. Quả thật là một sự kết hợp tuyệt vời giữa Toán học và Tin học đem đến ý nghĩa thực tiễn và ứng dụng cao cho cộng đồng.
Nhà toán học Anton Zorich thuộc Viện toán học Jussieu Paris đã viết: “Hai mươi năm trước, câu trả lời này hoàn toàn nằm ngoài tầm với; 10 năm trước cần một nỗ lực phi thường để viết hết những phần mềm cần thiết, chỉ tới bây giờ là thời điểm có thể đưa ra lời giải đáp”.
Vậy đấy, 4000 năm qua những khối đa diện đều đã xuất hiện trong những viên sỏi đá hay hình chạm khắc, hơn 2600 năm qua những tính chất toán học của chúng không ngừng được khám phá. Ngày hôm nay trên tay bạn là một hình khối lịch 12 tháng hiền hòa, xinh đẹp với những ngày tháng năm cụ thể. Nhưng biết đâu đấy, vẫn còn những bí ẩn nằm trong vũ trụ hài hòa ấy mà chúng ta còn chưa phát hiện ra!
Mùa Xuân đang đến, chúc các bạn một mùa Xuân an vui hiền hòa nhưng cũng chứa đựng rất nhiều đổi mới và không ngừng sáng tạo như vũ trụ kia bao la!
Phan Thị Hà Dương và Nguyễn Phúc Khánh Linh
Tài liệu tham khảo:
1. Mathematicians Report New Discovery About the Dodecahedron. (2020). Retrieved 1 February 2021, from https://www.quantamagazine.org/mathematicians-report-new-discovery-about-the-dodecahedron-20200831/
2. Khối đa diện đều Platon [Platonic solids]. (2021). Retrieved 2 February 2021, from https://vi.wikipedia.org/wiki/Kh%E1%BB%91i_%C4%91a_di%E1%BB%87n_%C4%91%E1%BB%81u_Platon
3. Mickael Launay. (2016). Toán học – Một thiên tiểu thuyết [Mathematics – A novel genius], Flammarion franchised Nha Nam Publishing, p. 69-71.
4. Hamiltonian path. (2021). Retrieved 8 February 2021, from https://en.wikipedia.org/wiki/Hamiltonian_path

