LTS: Ngày 17.3.2021 vừa qua, Viện Hàn lâm Khoa học và Văn chương Na Uy đã quyết định trao giải thưởng Abel (được ví như giải Nobel của Toán học) cho hai nhà toán học Avi Wigderson và László Lovász vì những đóng góp của họ trong Khoa học máy tính – Toán rời rạc và vai trò dẫn dắt của họ trong việc đưa các chuyên ngành này vào trung tâm của toán học hiện đại. Nhân sự kiện trên, PGS. Phan Thị Hà Dương (phòng Cơ sở Toán học của Tin học – Viện Toán học và Quỹ Đổi mới sáng tạo VinIF) đã kể câu chuyện về Các khối đa diện đều và các khám phá mang lại những ứng dụng sâu rộng trong cuộc sống – trong đó nhiều khám phá đạt được nhờ có toán rời rạc hoặc sức mạnh của tin học. LĐCT xin giới thiệu cùng bạn đọc.
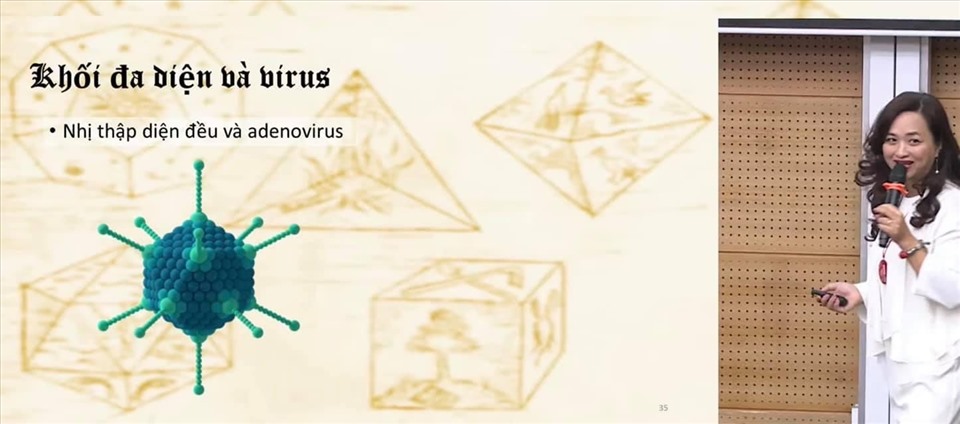
1. Con người tự cổ xưa cho đến ngày nay luôn khao khát kiến thiết nên những công trình hài hòa và bền vững. Để làm được điều đó, họ đã nghiên cứu, phân tích cấu trúc những khối hình cân đối nhất. Lạ kỳ thay, những công trình kiến trúc vĩ đại lại có cùng cấu trúc với những tạo vật vô cùng nhỏ bé của thiên nhiên, như mái vòm hùng vĩ La Géode tại Trung tâm Khoa học và Công nghệ Pháp có cùng cầu trúc với những con virus cúm nhỏ tinh vi. Nhưng thực ra điều lạ kỳ ấy có lẽ lại là một điều hiển nhiên vì cả hai được xây dựng từ một hình khối đều đặn nhất, khối đa diện đều 20 mặt. Vì sao lại là 20 mặt mà không nhiều hơn? Ta đã biết trên mặt phẳng có vô vàn đa giác đều, bao nhiêu cạnh cũng được. Vậy trong không gian có bao nhiêu khối đa diện đều – những hình khối mà các đỉnh, các cạnh và các mặt bằng nhau, đều đặn như con xúc xắc ta chơi trên bàn cờ? Nó đã được khám phá từ bao giờ?

Vào thời Hy Lạp cổ đại, những nhà Toán học cũng thường là những nhà triết học, thiên văn học và thậm chí cả chiêm tinh học nữa. Họ sẽ là những người ngắm những vì sao trên trời và vẽ nên những quỹ đạo, họ sẽ đo đạc các mảnh đất và tạo nên những hình vẽ và các con số, và họ sẽ thổi vào tất cả những ý nghĩa triết học sâu xa.
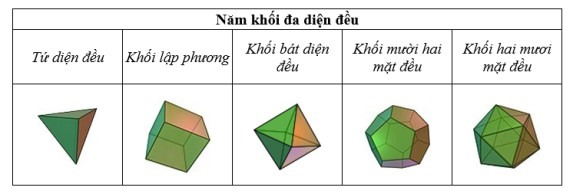
Platon (428/427 hay 424/423 – 348/347 TCN) đã là một người như thế. Ngày nay những khối đa diện đều, những tạo vật đẹp đẹp hài hòa nhất của không gian được mang tên ông vì ông đã mang đến cho chúng ý nghĩa triết học. Mặc dù rằng trước Platon, hơn 2000 năm TCN người cổ đại đã tạo ra những hình khối này mà dấu vết còn lưu lại trong các bào tảng. Bất ngờ thay, chỉ có 5 khối thôi, là những khối: 4 mặt, 6 mặt, 8 mặt, 12 mặt và 20 mặt. Platon đã gán chúng với 4 nguyên tố chính ngày ấy: Trái đất với hình lập phương, lửa với hình tứ diện, nước với hình nhị thập diện và không khí với hình bát diện. Còn lại hình 12 mặt, với dáng vẻ hài hòa đều đặn của nó, ông gán với vũ trụ, và ông viết: “Thượng đế đã dùng nó để thêu các vì sao lên bầu trời”.
Vào thời kỳ ấy khi các nhà toán học khám phá hình học (sau khi đã tìm hiểu về những con số) họ đã tin rằng hình học có sức mạnh vô song, đến nỗi Platon đã cho khắc trên cánh cổng trường học của mình: “Ai không hiểu về hình học thì không được bước chân vào đây”. Những người bước qua cánh cửa ấy đã được học trong những trường học Athens nơi tư duy được rộng mở, nơi những tranh luận đã làm khởi phát nhiều lý thuyết.

Cứ như vậy bao nhiêu thế kỷ trôi qua, các nhà khoa học vẫn luôn không ngừng suy ngẫm và khám phá nhiều điều trong cuộc sống từ những khối đa diện. Léonard de Vinci cũng đã viết nhiều cuốn sách về chúng. Nhưng có lẽ một trong những công trình đang kể nhất là cuốn Mysterium Cosmographicum – cuốn sách về Thiên văn của nhà thiên văn học vĩ đại Johannes Kepler (1571-1630). Ông đã là người phát triển lý thuyết của Copernic, người đã chỉ ra rằng không phải Trái đất là trung tâm và mặt trời cùng các vì sao quay quanh nó, mà chính là trái đất quay quanh mặt trời kia. Kepler đã xây dựng một mô hình vũ trụ xen kẽ 5 khối đa diện và 6 hình cầu, 6 hình cầu ấy được ông gắn với 6 vì tinh tú được biết đến lúc ấy là Sao Thủy, Sao Kim, Trái Đất, Sao Hỏa, Sao Mộc, Sao Thổ; và ông đã có những giả thuyết về tỉ lệ của các vì sao và tỉ lệ của các khối cầu.
Dẫu cho những tính toán này của Kepler không chính xác nhưng cuốn sách của ông đã có rất nhiều khám phá khác và đặt một dấu ấn trong lịch sử thiên văn học.
2. Nhưng có lẽ ta sẽ quay về một chút với câu hỏi, vì sao 5 khối mà không nhiều hơn, hay vô hạn? Một chứng minh rất đẹp dựa trên công thức nổi tiếng của Leonhard Euler (1707 – 1783). Công thức ấy là V-E+F=2 trong đó V, E, F lần lượt là số đỉnh, số cạnh và số mặt của khối đa diện. Công trình này đã nổi tiếng đến mức nó cùng với hình của Euler và khối nhị thập diện đều đã được in trên con tem của Đức.
Với những người làm tin học thì Euler nổi tiếng nhất lại vì ông chính là ông tổ của lý thuyết đồ thị. Đồ thị, đó có lẽ đã là một khái niệm ăn sâu vào muôn mặt cuộc sống trong thời đại bùng nổ kỹ thuật số hiện nay – như mạng xã hội, chữ mạng là network, chính nó đã mang nghĩa đồ thị. Lý thuyết đồ thị đã được xây dựng và phát triển mạnh mẽ trong TK 20 và chắc chắn sẽ bùng nổ trong TK 21, nhưng cội nguồn sâu xa của nó chính là bài toán 7 cây cầu ở Konigsberg của Euler. Ông đã đặt viên gạch đầu tiên cho lý thuyết đồ thị bằng cách định nghĩa chu trình Euler. Bài toán Euler cũng luôn được gắn chặt như một hình ảnh đối ngẫu với bài toán chu trình Hamilton – khái niệm được nhà toán học William Rowan Hamilton (1805 -1865) đặt ra dựa trên khối đa diện đều 12 mặt và 20 mặt. Hai bài toán này trở thành một phần cơ bản của lý thuyết Tin học, là ví dụ điển hình cho khái niệm cốt lõi nhất: Vấn đề P và NP – một vấn đề mà bất cứ người làm tin học nào cũng trăn trở và muốn khám phá.
Cùng với các vấn đề lý thuyết, có thể kể đến ứng dụng nổi trội của các khối đa diện trong kiến trúc, đặc biệt thông qua nhà thiết kế, sáng chế vĩ đại người Mỹ Buckminster Fuller. Khi ngắm mái vòm The Montreal Biosphere (Quebec, Canada) do Fuller thiết kế năm 1967, chúng ta khó có thể biết được mối liên hệ giữa nó và các khối đa diện đều, vì 5 khối chỉ có nhiều nhất là 20 mặt còn tòa nhà này gồm hàng trăm nghìn mảnh tam giác nhỏ. Nhưng không, chúng có một mối liên hệ mật thiết, và chính Fuller đã xây dựng nên lý thuyết kiến trúc để xây nên những mái vòm như vậy. Thật kỳ lạ sao, trước Fuller 7 thế kỷ, Đài quan sát Maragheh Observatory – Iran đã được thiết kế với cùng cấu trúc ấy. Và rồi, chúng ta còn thấy nó hiện diện ở khắp nơi, mà đẹp và nổi tiếng là tòa La Géode, ở Trung tâm Khoa học và Công nghệ Paris.

Nếu ta nhìn thật kỹ Đài quan sát Iran, ta sẽ thấy nó không hoàn toàn đều đặn, có những điểm kỳ dị trên đó. Dường như tất cả các đỉnh của nó đều là đỉnh của 6 tam giác. Nhìn thật kỹ, bạn sẽ thấy có 1 đỉnh bên phải thật đặc biệt, nó là đỉnh của 5 tam giác. Đó có phải là lỗi xây dựng không? Và có bao nhiêu lỗi như thế?

3. Fuller đã chỉ ra rằng đó chính là thiết kế, tất cả các công trình kể trên, dù to dù nhỏ, đều có đúng 12 điểm kỳ dị (nếu nó là mặt cầu hoàn chỉnh) vì tất cả đều được xây dựng từ khối nhị thập diện đều 20 mặt. Thật vậy, khi muốn dựng những hình cầu này, các KTS đã bắt đầu từ một hình đa diện gần giống hình cầu nhất, đó là hình nhị thập diện gồm 20 tam giác. Nhưng rõ ràng nó chưa phải hình cầu. Vậy thì ta sẽ chia nhỏ các cạnh ra. Nếu ta chia mỗi cạnh làm đôi thì mỗi tam giác sẽ có 4 tam giác nhỏ, và tưởng tượng ta thổi phồng từ trong ra thì sẽ có hình 80 mặt tam giác nhỏ, nó gần giống hình cầu hơn hình 20 mặt. Cứ như thế, người ta có thể chia 3, chia 4, chia 5… mỗi cạnh, càng chia nhỏ thì hình nhận được càng giống hình cầu. Nhận thấy là tất cả những điểm mới khi ta chia đều dính dưới 6 tam giác. Nhưng vẫn luôn còn đó 12 đỉnh đầu tiên chỉ đỉnh với 5 tam giác. Như vậy dù hình cầu ta to nhỏ cỡ nào, dù có trăm, nghìn, triệu đỉnh thì luôn có đúng 12 đỉnh kỳ dị.
Liệu rằng thiết kế đó có phải là đẹp nhất không? Có nhiều khi chúng ta tự hỏi những tác phẩm của ta có phải là điều đẹp nhất, hợp lý nhất? Tìm đâu ra câu trả lời? Có lẽ khi ấy ta hãy soi mình vào tự nhiên, bởi tự nhiên chính là tác phẩm của Thượng đế, và Thượng đế luôn tài hoa hơn con người. Vậy thì một sản phẩm của Thượng đế, dẫu đáng buồn nhưng ta phải chấp nhận, chính là virus adenovirus, nó cũng mang hình dáng được tạo ra từ khối nhị thập diện đều và nó cũng có 12 điểm kỳ dị. Bởi vì virus cũng cần phải có cấu trúc thật giản đơn, tiết kiệm năng lượng nhất và tồn tại bền vững. Và không chỉ nó, ngành vệ sinh dịch tễ đã xác nhận rất nhiều loài virus mang cấu trúc này. Chính những hiểu biết về khối đa diện đều đã giúp các nhà khoa học tìm hiểu cấu trúc của chúng.
Vậy đấy, các khối đa diện đã được nghiên cứu và đưa vào ứng dụng sâu rộng, tưởng rằng sẽ không còn làm ta ngạc nhiên nữa. Thế nhưng, mới đây nhất, năm 2019 và 2020, các công trình dài hơn 50 trang của các nhà khoa học Jayadev S. Athreya, David Aulicino, W. Patrick Hooper và Anja Randecker đã gây bất ngờ khi chứng minh rằng khối thập nhị diện khác với 4 khối còn lại như vũ trụ khác với 4 nguyên tố kia. Đó là kết quả về chu trình trắc địa, là một đường đi từ một đỉnh rồi quay về chính nó mà trên mỗi mặt nó là đoạn thẳng và khi đi từ mặt này qua mặt kia thì nó tạo các góc bằng nhau (tưởng tượng ta trải phẳng hai mặt ra, thì nó là đường thẳng). Đường trắc địa là một khái niệm quan trọng trong toán học, nó có nguồn gốc sâu xa từ việc đo đạc các đường đi ngắn nhất. Trước đó, các nhà bác học đã chứng minh rằng không có chu trình trắc địa cho 4 khối: 4, 6, 8, 20 mặt. Công trình năm 2020 nói trên đã có đóng góp to lớn trong việc nghiên cứu các đường trắc địa trên các khối đa diện đều nói riêng và nhiều hình khối nói chung, kết quả nổi trội của họ là đã chỉ ra rằng riêng với khối thập nhị diện tồn tại vô số chu trình trắc địa. Đây là một công trình kết hợp giữa các nghiên cứu toán học của mấy chục năm qua và sử dụng sức mạnh vượt trội của các thuật toán tin học hiện đại. Nhà toán học Anton Zorich – Viện toán học Jussieu Paris nhận định: “Hai mươi năm trước, câu trả lời này hoàn toàn nằm ngoài tầm với; 10 năm trước cần một nỗ lực phi thường để viết hết những phần mềm cần thiết, chỉ tới bây giờ là thời điểm có thể đưa ra lời giải đáp”.
Vậy là suốt 26 thế kỷ qua từ những triết lý và toán của Platon đến nay, các khối đa diện vẫn không ngừng mang đến những khám phá cho các nhà khoa học, để từ đó ứng dụng vào bao điều trong cuộc sống. Dẫu cho ta nghĩ rằng dáng hình vũ trụ có thể không phải là khối thập nhị diện đều như Platon đã hình dung, và nhiều lý thuyết của Platon, như khái niệm về Tình yêu thuần khiết (mà ngày nay ta gọi là tình yêu kiểu Platon) có thể bị cho là những điều mơ mộng và không thực tế; nhưng chính những điều mơ mộng ấy lại ẩn chứa bao bí mật và khơi nguồn bao sáng tạo.
(*) Bài viết sử dụng hơn 25 tài liệu tham khảo.
của PGS Phan Thị Hà Dương ở sự kiện hưởng ứng Ngày Toán học thế giới tại Hà Nội.
Phan Thị Hà Dương
Bài viết trên Báo Lao động cuối tuần (Báo giấy) và Báo Lao động Online

