Tìm hiểu về một Mô hình dự báo dịch Covid-19 từ Vũ Hán

Chúng tôi trình bày và giải thích về một mô hình dự báo ngắn hạn và dài hạn (gọi tắt là mô hình SEIR-C19) của việc lây lan dịch bệnh Covid-19 từ Vũ Hàn đến các tỉnh của Trung Quốc và quốc tế. Mô hình này do các tác giả GS. TS. Joseph T Wu, TS. Kathy Leung, GS. TS. BS. Gabriel M Leung (Trung tâm Hợp tác của WHO về Nghiên cứu dịch bệnh và Kiểm soát Bệnh truyền nhiễm, Khoa Y tế công cộng, Trường Y Li Ka Shing, Đại học Hồng Kông, Hồng Kông, Trung Quốc) thực hiện, và đăng trên tạp chí Lancet, xuất bản trực tuyến ngày 31/01/2020.

Mô hình cơ bản nhất về dịch bệnh là mô hình SIR của Kermack và McKendrick từ năm 1927 [1] và đã có rất nhiều biến thể của mô hình này cho các dịch bệnh khác nhau. Điểm đáng chú ý của mô hình SEIR của Wu et al. là đã xét những yếu tố sau:

• Có quá trình phơi nhiễm trước khi nhiễm bệnh.
• Nguồn bệnh từ người bệnh và cả từ động vật.
• Xét đến số lượng người di chuyển giữa Vũ Hàn và các vùng khác: vùng lân cận Vũ Hán và các vùng xa hơn.

Kết quả của mô hình được giới chuyên môn và nhiều bài báo chú ý được tóm lược như sau.

Kết quả: Trong kịch bản cơ sở, chúng tôi ước tính rằng hệ số lây nhiễm cơ bản của Covid-19 là 2,68 (CrI 95%: 2,47-2,86) và ở Vũ Hán tính đến 25/01/2020 đã có 75.815 người bị nhiễm (CrI 95%: 37.304-130.330). Thời gian tăng gấp đôi của dịch là 6,4 ngày (CrI 95%: 5,8-7,1). Chúng tôi ước tính rằng trong kịch bản cơ sở, số người bị lây nhiễm từ Vũ Hán ở Trùng Khánh, Bắc Kinh, Thượng Hải, Quảng Châu và Thâm Quyến lần lượt là 461 (CrI 95%: 227-805), 113 (57-193), 98 (49-168), 111 (56-191) và 80 (40-139). Nếu khả năng lây nhiễm của Covid-19 là giống nhau ở các địa phương và các thời điểm khác nhau, chúng tôi kết luận rằng dịch đã phát triển theo cấp số nhân ở nhiều thành phố lớn của Trung Quốc, với thời gian trễ (lag time) từ 1 đến 2 tuần so với sự bùng phát ở Vũ Hán.

Bài viết này chia làm hai phần:

• Phần 1: giới thiệu về mô hình dịch bệnh kinh điển SIR: giải thích và một số mô hình liên quan.
• Phần 2: mô hình SEIR-C19: chi tiết cách xây dựng mô hình, lấy số liệu, và kết quả của mô hình.

Phần 1: Mô hình dịch bệnh SIR

Mô hình SIR là một mô hình toán học cơ bản về dịch bệnh, được giới thiệu trong bài báo kinh điển của Kermack và McKendrick [11]. Trong mô hình này, dân số được chia thành 3 nhóm, dựa theo trạng thái đối với bệnh: 1) những người có khả năng mắc bệnh (Susceptible), 2) những người đang nhiễm bệnh và có thể lây cho người khác (Infected), và 3) những người không còn khả năng mắc bệnh (Removed hay Recovered). Trong mô hình này, trạng thái của một người chỉ có thể chuyển từ S sang I (nhiễm bệnh), hoặc từ I sang R (bình phục hoặc chết, nhưng không thể nhiễm lại).

Số người thuộc mỗi nhóm tại một thời điểm t được ký hiệu lần lượt là S(t), I(t) và R(t). Trong mô hình SIR đơn giản, tổng dân số được coi là không đổi, có nghĩa S(t) + I(t) + R(t) = N không phụ thuộc vào t. Đại lượng được quan tâm nhất là I(t): chiều tăng hay giảm (theo t) và độ lớn của nó cho biết xu hướng lây lan và quy mô của dịch bệnh.

Khi dân số N “đủ lớn”, sự vận động của hệ SIR có thể được xấp xỉ bằng hệ phương trình vi phân sau:

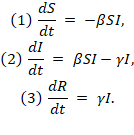
Các phương trình lần lượt biểu diễn tốc độ thay đổi (vế trái) của các đại lượng S, I và R tại thời điểm t theo trạng thái của hệ tại thời điểm đó (vế phải). Tham số β biểu diễn tỷ lệ lây nhiễm (theo đầu người), có thể được hiểu là xác suất (trung bình) để một người khỏe mạnh bị nhiễm bệnh (chuyển từ S sang I). Tham số γ biểu diễn tỷ lệ hồi phục, nói cách khác, khoảng thời gian mắc bệnh trung bình (tức là ở trong trạng thái I) là 1/γ.

Hệ số lây nhiễm cơ bản (R⁰)

Một trong những đại lượng quan trọng nhất đối với một mô hình dịch bệnh là hệ số lây nhiễm cơ bản, hay thường gọi là “hệ số R⁰”. Nếu R⁰ < 1, dịch sẽ tắt trước khi kịp bùng phát, còn nếu R⁰ > 1, dịch sẽ bùng phát. Thí dụ, trong mô hình SIR đơn giản ở trên, R⁰ = βN/γ, trong đó βN là số người khỏe mạnh trung bình mà một người mắc bệnh có thể lây cho trong khoảng thời gian mắc bệnh 1/γ [12, chương 2]. Một cách trực giác, điều này khá hợp lý: nếu trung bình một người mắc bệnh lây cho nhiều hơn một người thì số người mắc bệnh phải tăng (theo cấp số nhân), còn nếu trung bình một người mắc bệnh lây cho ít hơn một người khác thì số người mắc bệnh phải giảm dần.

Các mô hình tương tự

Trong mô hình SIR, một người sau khi khỏi bệnh không có nguy cơ mắc bệnh lại (không thể chuyển từ R sang S), do đó mô hình này thích hợp với những bệnh tạo thành miễn dịch sau khi khỏi. Với những bệnh không tạo thành miễn dịch hoặc chỉ có miễn dịch tạm thời, các mô hình SIS và tương ứng là SIRS sẽ được sử dụng. Các mô hình SEIR (dùng trong bài báo về Covid-19) và SEIS được sử dụng trong trường hợp khoảng thời gian mắc bệnh được chia thành hai giai đoạn nhỏ: chưa có khả năng lây cho người khác (Exposed – phơi nhiễm) và có khả năng lây cho người khác (Infected hay Infective). Những mô hình phức tạp hơn có thể tính đến nhiều yếu tố ngoài dịch bệnh ảnh hưởng đến dân số như tỷ lệ sinh, tỷ lệ chết tự nhiên, sự di cư, nhập cư giữa vùng có dịch và bên ngoài hoặc giữa các vùng có dịch với nhau, v.v.

Thí dụ, trong bài báo về dịch Covid-19 ở Vũ Hán, các tác giả đã sử dụng một mô hình SEIR (với một hệ thống ký hiệu hơi khác để phù hợp hơn với dữ liệu đầu vào) và có tính đến yếu tố di chuyển, cũng như nguồn lây nhiễm từ bên ngoài (động vật). Tham số γ trong đó chính là 1/D^I, tham số tương tự cho E(t) là 1/D^E, còn tỷ lệ lây nhiễm là β = R⁰/(ND^I).

Mô hình và kết quả mô phỏng

Việc giải ra công thức chính xác của I(t) theo t là hầu như không thể. Thay vào đó, người ta thường tìm lời giải số, với sự trợ giúp của máy tính. Tính hợp lý của mô hình được kiểm nghiệm bằng tính phù hợp của kết quả của mô phỏng với dữ liệu đã có, cũng như tính chính xác của các dự báo cho tương lai. Tuy nhiên, kết quả của mô phỏng có thể nhạy cảm với độ chính xác của dữ liệu đầu vào và đặc biệt là các giả định và tham số. Hai yếu tố sau đòi hỏi hiểu biết rõ về căn bệnh đang được nghiên cứu, do đó việc tìm ra một mô hình phù hợp cho một bệnh mới (như bệnh viêm phổi do Covid-19) luôn là một thách thức lớn.

Phần 2: Mô hình SEIR-C19 mô phỏng dịch Covid-19 ở Vũ Hán.

1. Mô hình và giải thích mô hình.

Mô hình: có nguy cơ – phơi nhiễm – nhiễm – hồi phục (SEIR) mô phỏng dịch ở Vũ Hán kể từ khi nó bắt đầu vào tháng 12/2019:

Các tham số và các biến:

• S(t) số người khỏe, E(t) số người phơi nhiễm, I(t) số người nhiễm ở thời điểm t,
• R(t) số người đã khỏi hoặc đã chết ở thời điểm t,
• D^E thời gian phơi nhiễm trung bình,
• D^I thời gian nhiễm trung bình,
• R⁰ hệ số lây nhiễm cơ bản; trung bình một người nhiễm có thể lây cho bao nhiêu người, làm cho họ bị phơi nhiễm (trong toàn bộ thời gian nhiễm bệnh của người đó),
• zt là nguồn lây nhiễm từ động vật, bằng 86 ca mỗi ngày trong kịch bản cơ sở trước khi chợ hải sản đóng cửa ngày 01/01/2020 và bằng 0 sau đó.
• L^W,I(t) (tương ứng, L^W,C(t)): số người từ Vũ Hán đến vùng lân cận (đến các thành phố khác).
• L^I,W(t) (tương ứng, L^C,W(t)): số người đến Vũ Hán từ vùng lân cận (từ các thành phố khác).

Ý nghĩa các tham số và các biến

• Một người khỏe (S) sẽ có thể bị phơi nhiễm (E) khi gặp một người nhiễm (I) (với hệ số R⁰ /N) hoặc khi gặp động vật,
• Một người phơi nhiễm (E) sẽ có khả năng bị nhiễm (I), trung bình sau D^E ngày,
• Một người nhiễm (I) sẽ có khả năng khỏi hoặc chết (R), trung bình sau D^I ngày.
• Tốc độ hổi phục thường được gọi là ɤ = 1/ D^I,
• Tốc độ lây lan thường được gọi là β = ɤ R⁰ / N = R⁰ / ND^I.

Hệ phương trình

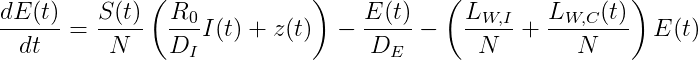
Giải thích các Phương trình:

Phương trình 3: I(t) số người bị nhiễm, và dI(t)/dt thể hiện số người bị nhiễm thêm ở ngày thứ t: (nếu quy ước đơn vị là ngày, dt= 1), thì dI(t)= I(t+1) – I(t). Đại lượng này được tính dựa trên 3 yếu tố:

• Tăng: số người bị phơi nhiễm trở thành bị nhiễm sau ngày t = số người bị phơi nhiễm ở ngày t chia cho số ngày bị phơi nhiễm = E(t)/ D^E
• Giảm: số người bị nhiễm đã khỏi (hoặc chết) sau ngày t = số người bị nhiễm ở ngày t chia cho số ngày bị nhiễm = I(t)/ D^I
• Giảm: số người bị nhiễm đi khỏi Vũ Hán (đến các vùng lân cận L^W,I(t), hoặc đến các thành phố khác L^W,C(t)): tính tổng số người này nhân với tỷ lệ nhiễm I(t)/N: vậy là (L^W,I(t)/N + L^W,C(t)/N) I(t).

Phương trình 2: E(t) thể hiện số người bị phơi nhiễm, và dE(t)/dt thể hiện số người bị nhiễm thêm ở ngày thứ t: nghĩa là E(t+1) – E(t). Đại lượng này được tính dựa trên các yếu tố:

• Tăng: Số người khỏe (có khả năng phơi nhiễm) trở nên phơi nhiễm = Khả năng người khỏe (S(t)/N) gặp nguồn bệnh, gồm:
  • Từ người nhiễm: hệ số lây nhiễm * người nhiễm chia số ngày bị nhiễm: R⁰* I(t)/ D^I
  • Từ động vật: z(t)
• Giảm: Số người phơi nhiễm trở thành nhiễm: E(t)/ D^E Giảm: số người bị phơi nhiễm đi khỏi Vũ Hán (đến vùng lân cận L^W,I(t), hoặc đến thành phố khác L^W,C(t)): tính tổng số người này nhân với tỷ lệ phơi nhiễm E(t)/N: vậy là (L^W,I(t)/N + L^W,C(t)/N) E(t).

Phương trình 1: S(t) thể hiện số người khỏe (có nguy cơ bị nhiễm), và dS(t)/dt thể hiện số người bị nhiễm thêm ở ngày thứ t: nghĩa là S(t+1) – S(t). Đại lượng này được tính dựa trên các yếu tố:

• Giảm: Số người khỏe (có khả năng phơi nhiễm) trở nên phơi nhiễm S(t)/N (R⁰ I(t)/ D^I + z(t) )
• Tăng: số người có khả năng phơi nhiễm đến khỏi Vũ Hán (từ các vùng lân cận L^W,I(t), hoặc từ các thành phố khác L^W,C(t)): L^I,W(t) + L^C,W(t)
• Giảm: số người có khả năng phươi nhiễm đi khỏi Vũ Hán (đến các vùng lân cận L^W,I(t), hoặc đến các thành phố khác L^W,C(t)): tính tổng số người này nhân với tỷ lệ nhiễm S(t)/N: vậy là (L^W,I(t)/N + L^W,C(t)/N) S(t).

Sau đây là cách ước lượng hệ số lây lan R⁰.

Giả định thói quen di chuyển không bị ảnh hưởng bởi bệnh dịch, do đó sự lây lan ra quốc tế xảy ra theo một quá trình không thuần nhất với tốc độ

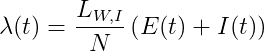
Từ đó, kỳ vọng của số ca lây ra quốc tế vào ngày d là

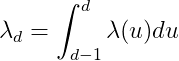
Hàm khả năng [likelihood function] là

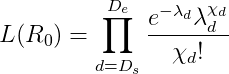
Ước lượng R⁰ bằng phương pháp Monte Carlo xích Markov với phép lấy mẫu Gibbs và xác suất tiên nghiệm không có thông tin [non-informative flat prior]. Với mỗi R⁰ nhận được từ phân phối hậu nghiệm, sử dụng cùng mô hình SEIR để ước lượng quy mô bùng phát dịch ở Vũ Hán và phân phối xác suất của số ca lây nhiễm đến các thành phố khác trong Trung Quốc đại lục (dựa trên phân phối điểm đến tính từ cơ sở dữ liệu di chuyển của Tencent). Các giá trị ước lượng là giá trị trung bình hậu nghiệm, và tính bất định thống kê được biểu diễn bằng các khoảng tin cậy 95%.

1. Số liệu:

• Dữ liệu về số ca lây nhiễm từ Vũ Hán tới các quốc gia: từ 31/12/2019 đến 28/01/2020 (phát hiện triệu chứng từ ngày 25/12/2019 đến ngày 19/01/2020) để tính số người bị nhiễm ở Vũ Hán từ ngày 01/12/2019 đến ngày 25/01/2020. Sau đó, chúng tôi ước lượng số ca lây nhiễm từ Vũ Hán sang các nơi khác ở Trung Quốc.
• Dự báo sự lây lan của 2019-nCoV ở Trung Quốc và trên toàn thế giới, có tính đến tác động của việc phong tỏa Vũ Hán và các thành phố lân cận từ ngày 23-24/01/2020.
• L^W,I(t), L^W,C(t), L^I,W(t), L^C,W(t) :dữ liệu đặt vé máy bay hàng tháng của Official Aviation Guide và dữ liệu di chuyển của dân ở hơn 300 thành phố Trung Quốc đại lục từ cơ sở dữ liệu Tencent.
• I(t): theo báo cáo đã công bố của Trung tâm Kiểm soát và Phòng ngừa Dịch bệnh Trung Quốc.
• D^I , D^E: ước lượng theo các nghiên cứu về (SARS-CoV).
• R⁰: được ước lượng bằng các phương pháp Monte Carlo xích Markov và được biểu diễn bằng giá trị trung bình hậu nghiệm và khoảng tin cậy (CrI) 95%.

1, Kết quả

Hình 2 tóm tắt các ước lượng về R⁰ và quy mô bùng phát dịch ở Vũ Hán tính đến 25/01/2020. Trong kịch bản cơ sở, ước lượng R⁰ là 2,68 (CrI 95%: 2,47 – 2,86) với khoảng thời gian nhân đôi của dịch bệnh là 6,4 ngày (CrI 95%: 5,8 – 7,1). Ước tính có 75815 người (CrI 95%: 37304 – 130330) đã nhiễm virus ở Vũ Hán và khu vực lân cận tính đến 25/01/2020. Ước tính số ca nhiễm mang từ Vũ Hán đến Trùng Khánh, Bắc Kinh, Thượng Hải, Quảng Châu và Thâm Quyến lần lượt là 461 (227 – 805), 113 (57 – 193), 98 (49 – 168), 111 (56 – 191) và 80 (40 – 139) (hình 3). Các thành phố Bắc Kinh, Thượng Hải, Quảng Châu và Thâm Quyến chiếm 53% lượng bay quốc tế từ Trung Quốc và 69% lượng bay quốc tế ra khỏi châu Á, trong khi Trùng Khánh có 32 triệu dân và có lượng giao thông đường bộ rất cao với Vũ Hán. Sự lây lan nhanh chóng của dịch ở các thành phố này sẽ góp phần khiến 2019-nCoV lan rộng trong và ngoài Trung Quốc đại lục.

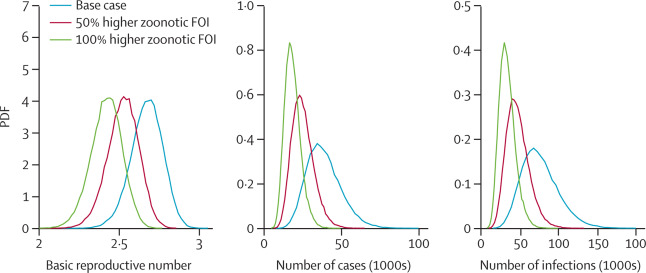
Ước lượng tính đến thời điểm 25/01/2020. Chỉ tính số ca biểu hiện triệu chứng hoặc có khả năng lây nhiễm. Số ca ở đây nhỏ hơn tổng số bị nhiễm vì một số người đã nhiễm nhưng còn trong thời gian ủ bệnh. Chúng tôi giả định người bệnh không có khả năng lây trong thời gian ủ bệnh (nghĩa là tương tự SARS-CoV [2]). PDF=probability density function (hàm mật độ xác suất). FOI=force of infection (nguồn lây nhiễm).

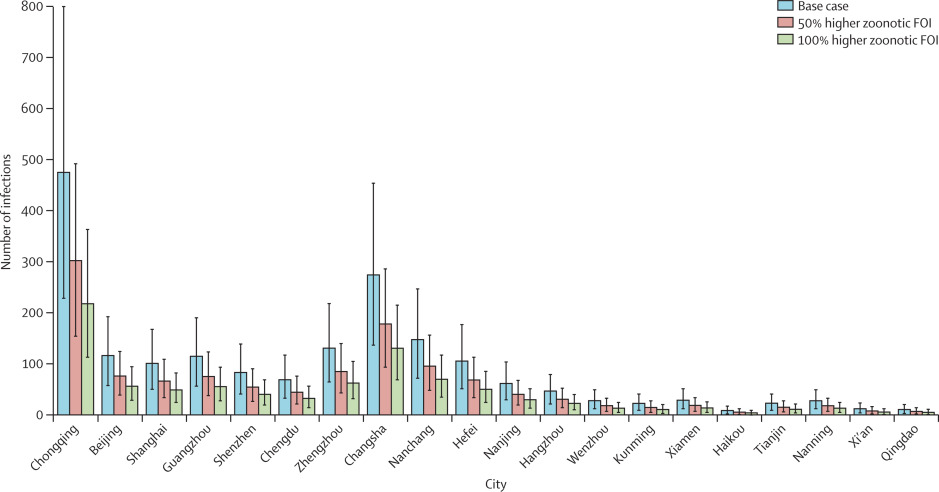
Ước lượng tính đến thời điểm 26/01/2020. Dữ liệu là trung bình hậu nghiệm với khoảng tin cậy 95%.

Nếu nguồn lây nhiễm từ động vật ban đầu ở Vũ Hán cao hơn kịch bản cơ sở 50% và 100%, thì các giá trị tương ứng của R⁰ lần lượt là 2,53 (CrI 95%: 2,32 – 2,71) và 2,42 (2,22 – 2,60). Ước lượng số ca nhiễm tương ứng ở Vũ Hán sẽ giảm lần lượt 38% và 56% so với kịch bản cơ sở. Số ca lây đến Trùng Khánh, Bắc Kinh, Thượng Hải, Quảng Châu và Thâm Quyến cũng giảm tương tự (hình 3).

Trong hình 4 là đồ thị bệnh dịch của Vũ Hán, Trùng Khánh, Bắc Kinh, Thượng Hải, Quảng Châu và Thâm Quyến với R⁰=2,68 và dưới các giả định khả năng lây nhiễm giảm 0%, 25%, 50% ở tất cả các thành phố, cùng với các giả định giao thông giữa các thành phố giảm 0% và 50% sau khi Vũ Hán bị đóng cửa ngày 23/01/2020. Dịch sẽ tắt dần nếu khả năng lây nhiễm giảm xuống dưới 1 – 1/R⁰=63%. Ước lượng của chúng tôi gợi ý rằng mức giảm 50% của giao thông giữa các thành phố có ảnh hưởng không đáng kể đối với sự phát triển của dịch bệnh. Chúng tôi dự đoán rằng nếu khả năng lây nhiễm không giảm, dịch ở Vũ Hán sẽ đạt đỉnh vào khoảng tháng 04/2020, và các dịch cục bộ ở các thành phố khác trong Trung Quốc đại lục sẽ đi sau từ 1 đến 2 tuần. Nếu khả năng lây nhiễm giảm 25% ở mọi thành phố trong nước, cả tốc độ phát triển lẫn quy mô của các dịch cục bộ sẽ giảm đáng kể; đỉnh dịch sẽ lùi lại khoảng 1 tháng và quy mô của nó giảm khoảng 50%. Khả năng lây nhiễm giảm 50% sẽ đưa hệ số lây nhiễm của virus xuống 1,3 và dịch sẽ tăng chậm mà không đạt đỉnh trong nửa đầu năm 2020. Tuy nhiên, mô phỏng của chúng tôi cho thấy cô lập hoàn toàn dân chúng cả Vũ Hán và khu vực lân cận có ảnh hưởng không đáng kể đối với chiều hướng tiếp theo của dịch, vì nhiều thành phố lớn ở Trung Quốc đã có hàng chục mầm lây nhiễm (chúng tôi không trình bày những kết quả này vì các đồ thị giống với hình 4). Xác suất để một chuỗi lây nhiễm bắt đầu từ một người kết thúc trước khi gây bùng phát dịch giảm nhanh khi R⁰ tăng (chẳng hạn xác suất nhỏ hơn 0,2 khi R⁰>2) [1,3]. Do vậy, với số ca nhiễm bệnh đã có từ Vũ Hán (hình 3), dịch cục bộ có thể đã đang phát triển theo cấp số nhân ở nhiều thành phố lớn của Trung Quốc. Và do Bắc Kinh, Thượng Hải, Quảng Châu và Thâm Quyến chiếm hơn 50% lượng di chuyển hàng không từ Trung Quốc đi quốc tế, các nước khác cũng có nguy cơ có dịch Covid-19 trong nửa đầu năm 2020.

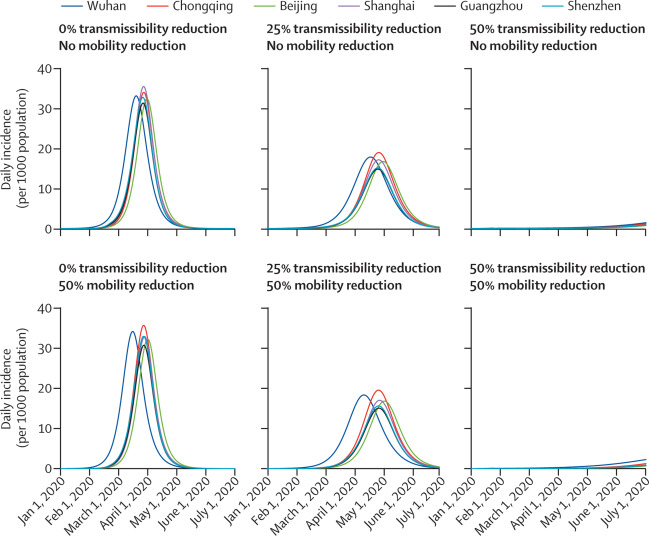
2. Thảo luận

Ưu tiên dịch tễ học quan trọng hàng đầu là thiết lập và công bố một danh sách các ca nghi ngờ, có thể, rất có thể và đã xác định nhiễm và những người tiếp xúc gần với họ; danh sách này cần được cập nhật hàng ngày và liên kết với các kết quả lâm sàng và kết quả xét nghiệm. Một danh sách tốt có vai trò cốt yếu để tìm ra các tham số dịch tễ học chính xác làm đầu vào cho các mô hình lây lan, để đưa ra cảnh báo theo tình huống và tối ưu hóa việc đối phó với dịch bệnh [6]. Ngoài ra, do mức độ lây lan và dư luận lo lắng mà Covid-19 đã gây ra, phổ lâm sàng và tính nghiêm trọng của nó cần nhanh chóng được tìm hiểu rõ bằng các phương pháp khách quan và đáng tin cậy trên những mẫu ngẫu nhiên của các ca nhiễm, đặc biệt là những ca có biểu hiện nhẹ hoặc cận lâm sàng.

Những kỹ thuật mô phỏng được sử dụng trong nghiên cứu này rất giống với những kỹ thuật được nhiều đồng nghiệp khác sử dụng với cùng mục đích mô tả sự phát triển của dịch Covid-19 (Zhanwei Du, Đại học Texas Austin, trao đổi cá nhân) [7, 8, 9, 10]. Sự thống nhất về phương pháp này ủng hộ tính đúng đắn của dự báo ngắn hạn và dài hạn của chúng tôi. Một điểm mạnh nữa của nghiên cứu này là các tham số của mô hình dựa trên những dữ liệu mới nhất của OAG và Tencent. Tuy nhiên, nghiên cứu vẫn có một số hạn chế. Thứ nhất, chúng tôi giả định rằng sự di chuyển không bị ảnh hưởng bởi dịch bệnh, và rằng mọi ca nhiễm sớm muộn đều biểu hiện triệu chứng (dù có thể rất nhẹ). Chúng tôi có thể đã đánh giá thấp quy mô bùng phát dịch ở vùng Vũ Hán, nếu những người có nguy cơ bị nhiễm cao lại ít đi ra thế giới hơn, hoặc nếu tỷ lệ các ca nhiễm không biểu hiện triệu chứng là đáng kể. Thứ hai, ước lượng khả năng lây nhiễm và quy mô bùng phát dịch của chúng tôi khá nhạy cảm với những giả định liên quan đến cơ chế lây nhiễm từ động vật dẫn đến dịch ở Vũ Hán.

Tài liệu tham khảo

1. Lloyd-Smith JO, Schreiber SJ, Kopp PE, Getz WM. Superspreading and the effect of individual variation on disease emergence. Nature 2005; 438: 355–59.
2. Centers for Disease Control and Prevention. Frequently asked questions about SARS. 2005. https://www.cdc.gov/sars/about/faq. html (accessed Jan 25, 2020).
3. Diekmann O, Heesterbeek JAP. Mathematical epidemiology of infectious diseases: model building, analysis and interpretation. Chichester: John Wiley, 2000.
4. Desai AN, Kraemer MUG, Bhatia S, et al. Real-time epidemic forecasting: challenges and opportunities. Health Secur 2019; 17: 268–75.
5. Polonsky JA, Baidjoe A, Kamvar ZN, et al. Outbreak analytics: a developing data science for informing the response to emerging pathogens. Philos Trans R Soc Lond B Biol Sci 2019; 374: 20180276.
6. Lipsitch M, Finelli L, Heffernan RT, Leung GM, Redd SC. Improving the evidence base for decision making during a pandemic: the example of 2009 influenza A/H1N1. Biosecur Bioterror 2011; 9: 89–115.
7. Imai N, Cori A, Dorigatti I, et al. MRC Centre for Global Infectious Disease Analysis: Wuhan coronavirus reports 1–3. January, 2020. https://www.imperial.ac.uk/mrc-global-infectious-disease-analysis/ news–wuhan-coronavirus (accessed Jan 25, 2020).
8. Read JM, Bridgen JRE, Cummings DAT, Ho A, Jewell CP. Novel coronavirus 2019-nCoV: early estimation of epidemiological parameters and epidemic predictions. medRxiv 2020; published online Jan 24. DOI:10.1101/2020.01.23.20018549 (preprint).
9. Liu T, Hu J, Kang M, et al. Transmission dynamics of 2019 novel coronavirus (2019-nCoV). bioRxiv 2020; published online Jan 26. DOI:10.1101/2020.01.25.919787 (preprint).
10. Zhao S, Ran J, Musa SS, et al. Preliminary estimation of the basic reproduction number of novel coronavirus (2019-nCoV) in China, from 2019 to 2020: a data-driven analysis in the early phase of the outbreak. bioRxiv 2020; published online Jan 24. DOI:10.1101/2020.01.23.916395 (preprint).
11. [1] W. O. Kermack and A. G. McKendrick, Contributions to the mathematical theory of epidemics part I, Proc. R. Soc. Edinb., A115, 700–721, 1927.
12. [2] F. Brauer, P. van den Driessche, J. Wu (editors), Mathematical Epidemiology, Springer-Verlag Berlin Heidelberg, 2008.

Nguyễn Hoàng Thạch và Phan Thị Hà Dương.

Biên tập: Lê Thị Lý.

(Ghi chú: các phần in nghiêng trong bài là dịch từ bài báo của Wu et al.)